Conocimiento previo
Para realizar este proyecto se requiere conocimiento previo de los siguientes temas, si aun no has trabajado con lo que se menciona en la siguiente tabla, allí están los links a los post para que puedas dar un repaso adicional o puedas recordar el conocimiento necesario para poder realizar este proyecto.
| Proyecto | Descripción |
|---|---|
| Regla del divisor de voltaje | Uno de los conceptos de circuitos en serie es la regla de divisor de voltaje, fundamental para entender como es el comportamiento del voltaje cuando tiene varias resistencias en serie. |
Puente Wheatstone
El puente Wheatstone es una configuración popular de un circuito electrico que se utiliza para medir resistencias desconocidas, donde se requiere la detección de pequeños cambios en una cantidad. Estos están constituidos por cuatro resistencias que forman un circuito cerrado, siendo una de ellas la resistencia bajo medida.
El puente de wheatstone se utiliza para detectar cambio de resistencias muy pequeños donde su principal aplicación son los sensores tipo resistivos los cuales la resistencia es demasiado pequeña para que un conversor de análogo a digital lo pueda detectar.
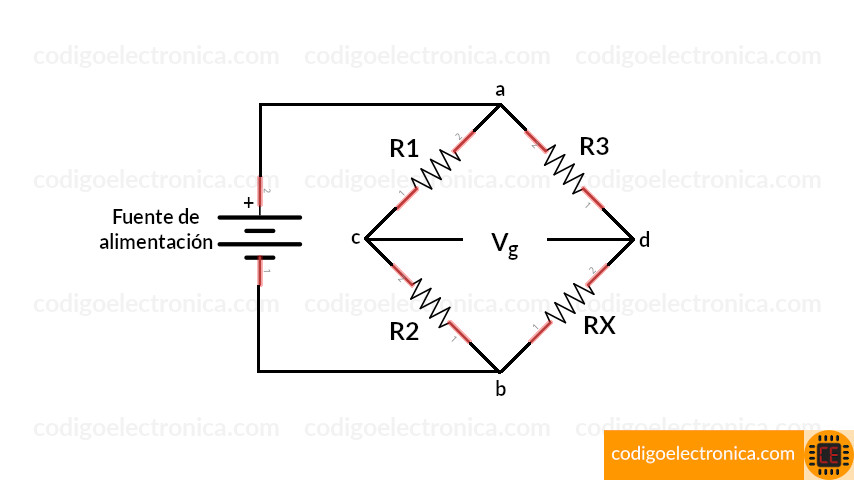
Lo que hacemos es utilizar ese cambio de resistencia muy pequeño en un voltaje que nosotros podamos medir o controlar desde cualquier circuito o microcontrolador.
En la imagen anterior podemos ver la configuración de este puente donde tenemos cuatro resistencias en forma de rombo, las podemos organizar como nosotros queramos normalmente vamos a encontrar este tipo de circuitos con esta forma, la característica de este circuito es que conocemos el valor de 3 resistencias (R1, R2, R3) y hay una resistencia que no conocemos su valor, adicionalmente podemos observar que tenemos una fuente de alimentación entre los puntos A y B, en los puntos C y D vamos a medir el voltaje que se encuentra allí para eso vamos a citar un multímetro.
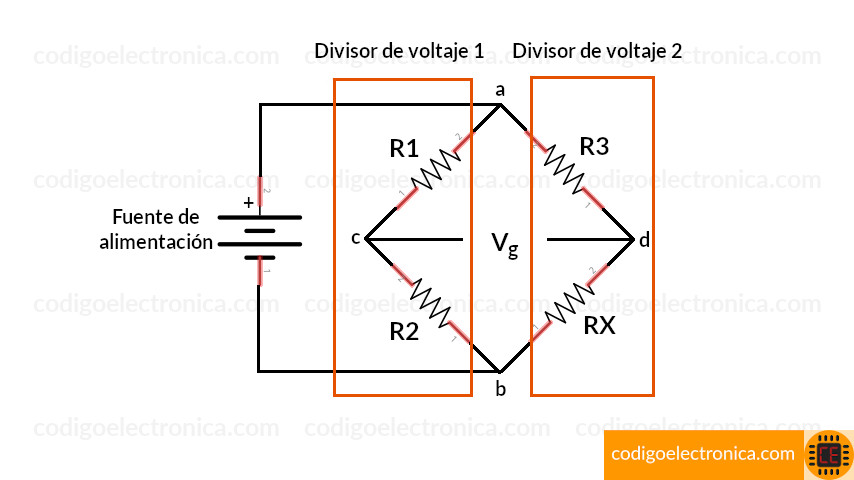
Observemos que el puente es básicamente dos circuitos divisores de voltaje conectados entre sí por los puntos A y B, entendiendo esto podemos realizar el siguiente análisis para determinar Cómo podemos obtener RX.
Vamos a realizar el siguiente análisis, vamos a determinar cual es la ecuación de cada uno de los circuitos divisores de voltaje para comenzar a despejar estas ecuaciones y poder determinar la resistencia en RX, así que la primera fórmula para que vamos a analizar es la siguiente:
Determinar cual es el voltaje del punto D para ello utilizaremos la fórmula que vimos en el divisor de voltaje, esta fórmula es la siguiente no le podemos observar que estamos utilizando las dos resistencias y el voltaje de entrada
Vamos a hacer lo mismo para determinar cual es el voltaje del punto C que en este caso vamos a utilizar la resistencia que nosotros necesitamos una resistencia que ya tenemos
Con las fórmulas anteriores lo que necesitamos determinar es la caída entre los voltajes C y D, decir qué voltaje CD es igual al resultado de voltaje en C menos voltaje en D estos expresan la siguiente fórmula:
Lo que intentamos hacer es obtener el equilibrio entre las dos fórmulas donde el voltaje en C y D sean igual a cero, esto quiere decir que voltaje en se va a ser igual a voltaje en de dónde lo podemos expresar con la siguiente ecuación
Con esto ya podemos empezar a reducir nuestra fórmula y nuestro primer paso es el siguiente Cómo podemos observar que voltaje de entrada 5 se encuentra en las desigualdades, así que los podemos cancelar donde nos va a quedar lo siguiente:
El siguiente paso es realizar una multiplicación cruzada donde vamos a obtener el siguiente resultado para la igualdad
Pasamos todos los valores de rx al lado derecho como se observa en la siguiente ecuación
Ahora decimos que RXR2 - RXR2 = 0 dónde podemos simplificar la ecuación de la siguiente forma y tenemos el siguiente resultado
Ahora al terminar de despejar la ecuación nos va a quedar ese resultado
Referencias
[1] Boylestad Introducción al analisis de circuitos de Boylestad decima edición, Consultado Diciembre 2020